Phillips–Perron test

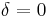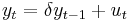In statistics, the Phillips–Perron test (named after Peter C. B. Phillips and Pierre Perron) is a unit root test. That is, it is used in time series analysis to test the null hypothesis that a time series is integrated of order 1. It builds on the Dickey–Fuller test of the null hypothesis $\delta = 0$ in Δ $y_{t}= \delta y_{t-1}%2Bu_{t}\,$ , where Δ is the first difference operator. Like the augmented Dickey–Fuller test, the Phillips–Perron test addresses the issue that the process generating data for 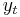$y_{t}$ might have a higher order of autocorrelation than is admitted in the test equation - making 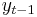$y_{t-1}$ endogenous and thus invalidating the Dickey–Fuller t-test. Whilst the augmented Dickey–Fuller test addresses this issue by introducing lags of Δ 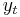$y_{t}$ as regressors in the test equation, the Phillips–Perron test makes a non-parametric correction to the t-test statistic. The test is robust with respect to unspecified autocorrelation and heteroscedasticity in the disturbance process of the test equation.

Davidson and MacKinnon (2004) report that the Phillips-Perron test performs worse in finite samples than the augmented Dickey-Fuller test.

Reference

Davidson, Russell and James G. MacKinnon (2004), Econometric Theory and Methods, p.623, ISBN 978-0195123722
Phillips, P.C.B and P. Perron (1988), "Testing for a Unit Root in Time Series Regression", Biometrika, 75, 335–346